Approche théorique du calcul intégral

Autres leçons de mathématiques

Département

Analyse

 

Interwikis

Rappel sur l'intégrale de Riemann

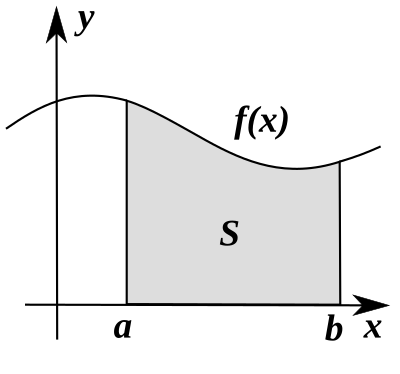
Le calcul d'intégrales au sens de Riemann correspond au calcul de l'aire comprise entre l'axe des abscisses et la courbe d'une fonction f donnée entre deux bornes a et b. Sa définition repose sur une suite de fonctions en escaliers convergeant vers f sur le segment [a,b]. En d'autres termes :

Soit f une fonction continue définie sur le segment [a,b]. On définit l'intégrale de a à b de la fonction f par $\int _{a}^{b}f(x)\mathrm {d} x=\lim _{n\rightarrow +\infty }{\frac {b-a}{n}}\sum _{k=0}^{n-1}f\left(a+{\frac {b-a}{n}}k\right)$

Grossièrement, cela revient à :

• « découper » le segment [a,b] en petits morceaux
• construire des rectangles s'appuyant sur chaque portion de segment ainsi que sur la courbe de f
• approcher l'intégrale de f par la somme des aires des rectangles.

Cette « approximation » est d'autant meilleure que le nombre de divisions du segment [a,b] augmente.

Intégrale double

On peut généraliser l’idée précédente à des problèmes à plusieurs dimensions. Par exemple, au lieu de considérer les contributions de points présents sur une ligne, on peut considérer la contribution de points d'une surface.

Soit une surface élémentaire d'ordre 2 $\mathrm {d} ^{2}S=\mathrm {d} x~\mathrm {d} y$ au voisinage de M.

Pour trouver la superficie totale, il faut sommer les contributions de tous les points de Σ. Comme cette somme se fait dans deux dimensions (x et y), il faut intégrer deux fois :

• Pour un y donné, on somme les contributions de tous les points M(x,y) tels que M soit dans Σ (intégrale suivant x). La surface infinitésimale d'ordre 1 dS, de largeur dy et de longueur x₂(y)-x₁(y) : $\mathrm {d} {\vec {S}}(y)=-\mathrm {d} y\int _{x_{1}(y)}^{x_{2}(y)}~\mathrm {d} x~{\vec {z}}$

• On fait ensuite l'intégrale sur y pour sommer les contributions de toutes les bandes horizontales. On obtient au final ${\vec {S}}=\int _{y_{min}}^{y_{max}}\mathrm {d} {\vec {S}}(y)=-\int _{y_{min}}^{y_{max}}\int _{x_{1}(y)}^{x_{2}(y)}~\mathrm {d} x\mathrm {d} y~{\vec {z}}$.

Cette dernière expression rend compte de la somme des contributions de tous les points de la surface Σ, de dimension 2. Pour condenser l'écriture, on utilise une intégrale double pour noter ${\vec {S}}=\iint _{\Sigma }-~\mathrm {d} x\mathrm {d} y~{\vec {z}}$.

On peut bien entendu choisir de faire l'opération dans l'autre sens : intégrer suivant y à x choisi, puis sur x.

Référents

Ces personnes sont prêtes à vous aider concernant ce cours :

• Loïc Fabiou (discuter)

cette liste