Probabilités et analyse combinatoire/Loi de Student

Début de la boite de navigation du chapitre

La loi de Student est une loi de probabilité, faisant intervenir le quotient entre une variable suivant une loi normale centrée réduite et la racine carrée d’une variable distribuée suivant la loi du χ².

fin de la boite de navigation du chapitre

Loi de Student

Densité de probabilité / Fonction de masse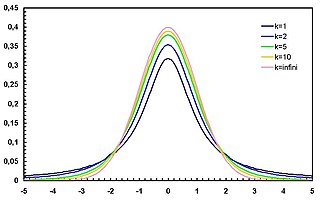
Fonction de répartition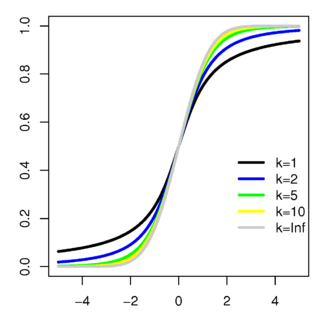
Paramètres	k ≥ 1 degrés de liberté,
Support	$x\in ]-\infty ;+\infty [$
Densité de probabilité (fonction de masse)	$f_{T}(t)={\frac {1}{\sqrt {k\pi }}}{\frac {\Gamma ({\frac {k+1}{2}})}{\Gamma ({\frac {k}{2}})}}{\frac {1}{(1+{\frac {t^{2}}{k}})^{\frac {k+1}{2}}}}$
Fonction de répartition	1-γ = ƒ(tγk), voir tableau en fin d'article
Espérance	si k = 1 : non définie si k > 1 : 0
Médiane (centre)	0
Mode	0
Variance	si k ≤ 2 : $+\infty$ si k > 2 : ${\frac {k}{k-2}}$
Asymétrie (skewness)	$0$ pour $\nu >3$
Kurtosis (non-normalisé)
Entropie
Fonction génératrice des moments
Fonction caractéristique

Soient Z une variable aléatoire de loi normale centrée et réduite et U une variable indépendante de Z et distribuée suivant la loi la loi du χ² à k degrés de liberté. Par définition la variable

$T={\frac {Z}{\sqrt {U/k}}}$

suit une loi de Student à k degrés de liberté.

La densité de T notée ƒ_T est :

$f_{T}(t)={\frac {1}{\sqrt {k\pi }}}{\frac {\Gamma ({\frac {k+1}{2}})}{\Gamma ({\frac {k}{2}})}}{\frac {1}{(1+{\frac {t^{2}}{k}})^{\frac {k+1}{2}}}},$ pour k ≥ 1.

où Γ est la fonction Gamma d'Euler.

La densité ƒ_T associée à la variable T est symétrique, centrée sur 0, en forme de cloche.

Son espérance ne peut pas être définie pour k = 1, et est nulle pour k > 1.

Sa variance est infinie pour k ≤ 2 et vaut ${\frac {k}{k-2}}$ pour k > 2.

Comportement limite

Lorsque k est grand, la loi de Student peut être approchée par la loi normale centrée réduite.

Application : détermination rigoureuse de l’intervalle de confiance associé à l’espérance d’une variable de loi normale de variance inconnue

Ce chapitre présente une méthode faisant appel à la loi de Student afin d’estimer l’espérance μ d’une loi normale dont la variance σ² est supposée inconnue.

Soient x₁…, x_n n variables indépendantes distribuées suivant une même loi normale d’espérance μ (à déterminer) et de variance σ² (inconnue).

Afin de parvenir au résultat, il est nécessaire d’introduire les variables ${\overline {x}}$ et s.

Soit

${\overline {x}}={\frac {1}{n}}\Sigma _{i=1}^{n}x_{i}$

La variable ${\overline {x}}$ suit la loi normale d’espérance μ et de variance ${\frac {\sigma ^{2}}{n}}$.

Soit

$s=\Sigma _{i=1}^{n}{\frac {(x_{i}-{\overline {x}})^{2}}{\sigma ^{2}}}$

La variable aléatoire s suit la loi du χ² à n - 1 degrés de liberté.

Remarque : ce résultat utile se démontre à partir de la propriété définissant la loi du χ² en tant que somme des carrés de variables normales centrées et réduites indépendantes 2 à 2, mais il n’en est pas pour autant la conséquence directe : en particulier les variables $x_{1}-{\overline {x}},\ldots ,x_{n}-{\overline {x}}$ ne sont pas indépendantes entre elles.

Pour n grand, la variance ${\frac {\sigma ^{2}}{n}}$ de ${\overline {x}}$ tend vers 0, et la valeur d’une réalisation de ${\overline {x}}$ constitue ainsi une estimation de l’espérance μ, qui est également l’espérance de la loi normale suivie par les variables x₁…, x_n. Néanmoins, seule la connaissance préalable de la variance σ² de cette loi permet de caractériser un intervalle de confiance pour la variable ${\overline {x}}-\mu$.

Par contre, il est possible de caractériser un intervalle de confiance rigoureux pour la variable suivante :

$T_{0}={\frac {{\overline {x}}-\mu }{\sqrt {S/n}}}$

avec

$S={\frac {s\sigma ^{2}}{n-1}}={\frac {1}{n-1}}\Sigma _{i=1}^{n}(x_{i}-{\overline {x}})^{2}$

En effet, moyennant quelques simplifications, la variable T₀ peut se réécrire comme

$T_{0}={\frac {Z}{\sqrt {s/(n-1)}}}$

avec

$Z={\frac {{\overline {x}}-\mu }{\sigma /{\sqrt {n}}}}$.

la variable Z suit la loi normale centrée et réduite, et nous avons vu ci-dessus que la variable s suit la loi du χ² à n - 1 degrés de liberté. De plus, il est possible de démontrer que Z et s sont indépendantes. Par définition, T₀ suit donc la loi de Student à k = n - 1 degrés de liberté.

La distribution de la variable T₀ est donc connue indépendamment de σ², et par conséquent les intervalles de confiance qui lui sont associés sont également connus. Ainsi, il est possible d’obtenir un intervalle de confiance pour μ à partir d’une réalisation des variables x₁…, x_n, de laquelle on déduit des valeurs de ${\overline {x}}$ et S. La suite de ce chapitre détaille la procédure permettant la détermination de cet intervalle de confiance.

Pour une variable T suivant la loi de Student à k degrés de liberté, on définit t_γ^k comme

la quantité telle que la probabilité d’obtenir T > t_γ^k soit égale à γ.

Ceci revient à imposer que 1-γ soit l'image de t_γ^k par la fonction de répartition de la loi de Student. La quantité t_γ^k est également appelé le quantile d’ordre 1-γ de la loi de Student à k degrés de liberté (voir tableau des valeurs de t_γ^k ci-dessous).

Dans ce cadre, si t_γ^k > 0, alors la probabilité d’obtenir -t_γ^k < T₀ < t_γ^k est égale à 1-2γ.

Or on a

$\mu ={\overline {x}}-T_{0}{\sqrt {\frac {S}{n}}}$.

La probabilité d’obtenir ${\overline {x}}-t_{\gamma }^{n-1}{\sqrt {\frac {S}{n}}}<\mu <{\overline {x}}+t_{\gamma }^{n-1}{\sqrt {\frac {S}{n}}}$ est elle aussi égale à 1-2γ. Le niveau de confiance α associé à cet intervalle est donc α = 1-2γ.

Le niveau de confiance α correspond à la probabilité que l’espérance μ de la loi normale se trouve à l’intérieur de l’intervalle de confiance. Par exemple pour α = 0,95, on a un niveau de confiance de 95 %, correspondant à γ = (1-α)/2 = 0,025.

Niveau de confiance α et γ

Intervalle de confiance α	γ
68 %	0,16
76 %	0,12
90 %	0,05
95 %	0,025
99 %	0,005
99,7 %	0,001 5
99,9 %	0,000 5
99,999 999 8 %	0,000 000 001

La courbe ci-dessous illustre la notion de niveau de confiance en représentant celui-ci comme une intégrale (aire de la zone en bleu).

Dans la courbe ci-dessus, les frontières entre la zone centrale et les deux zones latérales identiques correspondent à t = t_γ^k et t = -t_γ^k.

En résumé, l’intervalle de confiance de l’espérance μ d’une loi normale de variance quelconque inconnue peut être déterminé à partir des valeurs de n variables indépendantes x₁…, x_n suivant toutes cette même loi. Pour un niveau de confiance donné α, cet intervalle est le suivant :

$\left[\,{\overline {x}}-t_{(1-\alpha )/2}^{n-1}{\sqrt {\frac {S}{n}}},{\overline {x}}+t_{(1-\alpha )/2}^{n-1}{\sqrt {\frac {S}{n}}}\,\right]$,

avec

${\overline {x}}={\frac {1}{n}}\Sigma _{i=1}^{n}x_{i}$,

$S={\frac {1}{n-1}}\Sigma _{i=1}^{n}(x_{i}-{\overline {x}})^{2}$,

et

t_γ^k le quantile d’ordre 1-γ de la loi de Student à k degrés de liberté (dont la définition exacte est donnée ci-dessus).

Tableau des valeurs du quantile

Un tableau des valeurs du quantile en fonction de γ et k est fourni ci-dessous.

	γ
k	0,25	0,20	0,15	0,10	0,05	0,025	0,010	0,005	0,002 5	0,001 0	0,000 5
1	1,000	1,376	1,963	3,078	6,314	12,71	31,82	63,66	127,3	318,3	636,6
2	0,816	1,061	1,386	1,886	2,920	4,303	6,965	9,925	14,09	22,33	31,60
3	0,765	0,978	1,250	1,638	2,353	3,182	4,541	5,841	7,453	10,21	12,92
4	0,741	0,941	1,190	1,533	2,132	2,776	3,747	4,604	5,598	7,173	8,610
5	0,727	0,920	1,156	1,476	2,015	2,571	3,365	4,032	4,773	5,893	6,869
6	0,718	0,906	1,134	1,440	1,943	2,447	3,143	3,707	4,317	5,208	5,959
7	0,711	0,896	1,119	1,415	1,895	2,365	2,998	3,499	4,029	4,785	5,408
8	0,706	0,889	1,108	1,397	1,860	2,306	2,896	3,355	3,833	4,501	5,041
9	0,703	0,883	1,100	1,383	1,833	2,262	2,821	3,250	3,690	4,297	4,781
10	0,700	0,879	1,093	1,372	1,812	2,228	2,764	3,169	3,581	4,144	4,587
11	0,697	0,876	1,088	1,363	1,796	2,201	2,718	3,106	3,497	4,025	4,437
12	0,695	0,873	1,083	1,356	1,782	2,179	2,681	3,055	3,428	3,930	4,318
13	0,694	0,870	1,079	1,350	1,771	2,160	2,650	3,012	3,372	3,852	4,221
14	0,692	0,868	1,076	1,345	1,761	2,145	2,624	2,977	3,326	3,787	4,140
15	0,691	0,866	1,074	1,341	1,753	2,131	2,602	2,947	3,286	3,733	4,073
16	0,690	0,865	1,071	1,337	1,746	2,120	2,583	2,921	3,252	3,686	4,015
17	0,689	0,863	1,069	1,333	1,740	2,110	2,567	2,898	3,222	3,646	3,965
18	0,688	0,862	1,067	1,330	1,734	2,101	2,552	2,878	3,197	3,610	3,922
19	0,688	0,861	1,066	1,328	1,729	2,093	2,539	2,861	3,174	3,579	3,883
20	0,687	0,860	1,064	1,325	1,725	2,086	2,528	2,845	3,153	3,552	3,850
21	0,686	0,859	1,063	1,323	1,721	2,080	2,518	2,831	3,135	3,527	3,819
22	0,686	0,858	1,061	1,321	1,717	2,074	2,508	2,819	3,119	3,505	3,792
23	0,685	0,858	1,060	1,319	1,714	2,069	2,500	2,807	3,104	3,485	3,767
24	0,685	0,857	1,059	1,318	1,711	2,064	2,492	2,797	3,091	3,467	3,745
25	0,684	0,856	1,058	1,316	1,708	2,060	2,485	2,787	3,078	3,450	3,725
26	0,684	0,856	1,058	1,315	1,706	2,056	2,479	2,779	3,067	3,435	3,707
27	0,684	0,855	1,057	1,314	1,703	2,052	2,473	2,771	3,057	3,421	3,690
28	0,683	0,855	1,056	1,313	1,701	2,048	2,467	2,763	3,047	3,408	3,674
29	0,683	0,854	1,055	1,311	1,699	2,045	2,462	2,756	3,038	3,396	3,659
30	0,683	0,854	1,055	1,310	1,697	2,042	2,457	2,750	3,030	3,385	3,646
40	0,681	0,851	1,050	1,303	1,684	2,021	2,423	2,704	2,971	3,307	3,551
50	0,679	0,849	1,047	1,299	1,676	2,009	2,403	2,678	2,937	3,261	3,496
60	0,679	0,848	1,045	1,296	1,671	2,000	2,390	2,660	2,915	3,232	3,460
80	0,678	0,846	1,043	1,292	1,664	1,990	2,374	2,639	2,887	3,195	3,416
100	0,677	0,845	1,042	1,290	1,660	1,984	2,364	2,626	2,871	3,174	3,390
120	0,677	0,845	1,041	1,289	1,658	1,980	2,358	2,617	2,860	3,160	3,373
∞	0,674	0,842	1,036	1,282	1,645	1,960	2,326	2,576	2,807	3,090	3,291

Remarque : la dernière ligne du tableau ci-dessus correspond aux grandes valeurs de k. Il s’agit d’un cas limite pour lequel la loi de Student est équivalente à la loi normale centrée et réduite.

Voir aussi

Articles connexes

• Erreur
• Loi de Pearson IV

Liens externes

[pdf] • [licence inconnue] • La langue de ce document n’est pas renseignée ou inconnue • lien vers le document • La Loi du khi-2, la loi de Student, la loi de Fisher, Université Laval, Département de mathématiques et de statistique

Ce document en français contient en particulier la dérivation de l’expression de la densité de probabilité ƒ_T, la démonstration de la distribution de la variable s suivant la loi de Student à n-1 degrés de liberté, ainsi que la démonstration de l'indépendance de s et Z.

Probabilités, statistiques et analyses multicritères, M.Rouaud, révision 2017. Expressions et étude des premières Students, démonstration de l'expression de la variance et somme de Students indépendantes. La démonstration pour la variance est assez longue, elle figure pages 278 à 280.