1. Montrer qu'un écoulement conserve la masse revient à démontrer que l'écoulement est incompressible.
Le champ des vitesses d'Euler de l'écoulement proposé est donné par :

Montrer qu'un écoulement est incompressible, c’est montrer que la divergence de sa vitesse est nulle.
Par définition de la divergence on a,

Ce qui donne dans notre cas:

|
L'écoulement est incompressible donc il conserve la masse.
|
2. Retrouver les équations des lignes de courant revient à intégrer la relation suivante :

Dans notre cas, v_z est nulle : il faut intégrer la relation :

On a :


Soit : 
Avec :  et
et

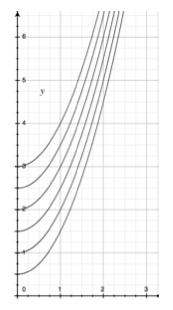
Le temps est ici considérer comme une constante car les lignes de courant sont tracer à un instant t fixé.
3. Par définition de l'accélération d'Euler, on a :

Le choix de l'une ou l'autre formule permet bien entendu d'arriver au même résultat. Il est plus commode d’utiliser l'une ou l'autre selon la situation. On apprendra à déceler les situations qui se prêtent le mieux à chacune des équations au fur et mesure que l'ont traitera des cas différents.
d'où 
et donc  Soit
Soit 

















