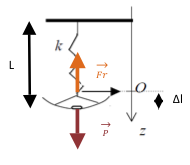
1. On peut écrire l'équation suivante grâce au principe fondamental de la statique :




2.On prend en compte dans ce cas l'action de la poussé d'Archimède  exercé par l'air sur la pépite d'or.
exercé par l'air sur la pépite d'or.
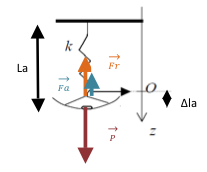
Dans ce cas, on est à l'équilibre aussi et d’après le principe fondamental de la statique :

Avec : 


Donc 
Soit : 
Remarque : La poussée d'Archimède n'étant pas prise en compte dans le calcul car celle-ci impact déjà le réglage du 0 dans la première question.
4. Dans le cas où l’on prend en compte la poussée d'Archimède, on considère que la force  (de réaction du ressort) correspond au poids apparent de la pépite d'or soumis à l'action de l'air.
(de réaction du ressort) correspond au poids apparent de la pépite d'or soumis à l'action de l'air.
On peut reprendre l’expression précédente :

On en déduit donc que :


Avec M la masse d'air déplacée par la pépite d'or et m la masse de la pépite d'or
Soit :

On défini alors l'écart relatif par : 


A.N :

4. Utilisation de la balance à plateau
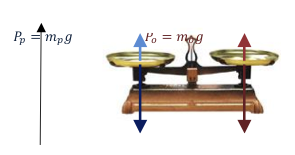
On isole le plateau, les pépites d'or et les masses en platine. On néglige le poids de la balance qui s'équilibre de par sa géométrie symétrique. On applique le principe fondamental de la statique et on obtient l'équation suivante des moments projetés sur l'axe Z :

Avec :
- L = distance du centre de gravité de la pépite au centre de la balance
-  = la poussée d'Archimède agissant sur la masse en platine
-
= la poussée d'Archimède agissant sur la masse en platine
-  = la poussée d'Archimède agissant sur la masse d'or
-
= la poussée d'Archimède agissant sur la masse d'or
-  = la masse de platine
-
= la masse de platine
-  = la masse de la pépite d'or
= la masse de la pépite d'or
Or :


D'où :

Puis :

Or :


Donc :

Finalement :

Remarque :Si l’on n'avait pas pris la poussée d'Archimède en compte on aurait eu :

On en déduit alors l'écart relatif tel que :


Conclusion : Donc l’utilisation d'une balance à plateaux et de masses étalonnées en platine permet une détermination plus précise de la masse de la pépite d'or.








































