Utilisateur:MathiasDlb/Modélisation des Réseaux (M1 SIREN, 2020)/Activité D
1)
Le nouveau réseau projeté :
Le tableau des degrés et nœuds :
Degré Nombre de nœuds Louise 3 2 Daphné 3 3 Mathias 4 3 Elsa 5 4 Auriane 5 4
Sous forme de diagramme :
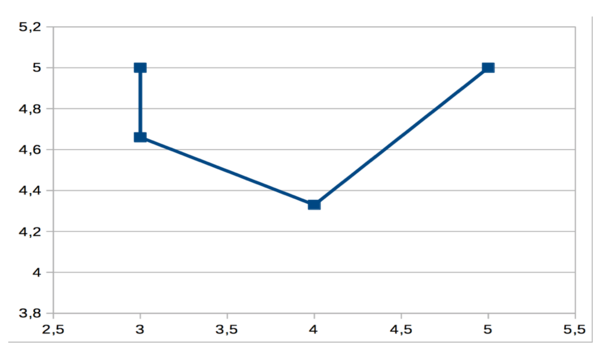
2) Pour calculer la corrélation suit le calcul suivant : C(noeud) = (sommes des degrés des nœuds voisins)/(nombre de nœuds voisins).
Ce qui donne :
Degré Degré voisins Louise 3 5 Daphné 3 4,66 Mathias 4 4,33 Elsa 5 5 Auriane 5 5
Et le graphique :
3)On peut dire que le réseau est assortatif car la corrélation entre les degrés de ses sommets et ceux de leurs voisins est élevée
4) Voici le coefficient de clustering des noeuds :
Nœud Coefficient de clustering Louise Daphné Mathias Elsa Auriane
5) Voici la corrélation combinée entre degré et coefficient de clustering :
Degré Corrélation combinée (degré, coefficient de clustering) 3 4 5
6) Avec cette courbe, on peut observer une distribution décroissante de degrés. Les degrés les plus bas sont connectés aux nœuds de degrés plus importants.
7) Le nœud Elsa a un coefficient de clustering plus petit que 1. En ajoutant un lien entre Mathias et Louise ainsi que Mathias et Daphné, le coefficient serait de 1.
8)Le noeud Louise a un coefficient de clustering de 1. Le réseau est constitué de 10 liens actuellement. En retirant les liens doubles on passe à 8. On peut ensuite retirer les 3 liens entre : Daphné et Mathias, Daphné et Auriane et mathias et Elsa. On peut donc retirer au maximum 5 liens.
9) La proximité étant l'inverse de la somme des distances, on a les valeurs suivantes :
Nœud Proximité Louise Daphné Mathias Elsa Auriane
On voit que Louise est le noeud avec la plus petite proximité et que les nœuds Auriane et Elsa sont ceux avec la plus grande proximité.
Pour l’intermediarité, on trouve les résultats suivants en effectuant, pour un nœud, la somme des rapports entre les chemins qui passent par ce nœud et le nombre de chemins les plus courts entre tous les autres nœuds du graphe. Ou comme expliquer bien mieux sur wikipedia, de cette façon :
« où est le nombre de plus courts chemins de à et est le nombre de tels chemins passant par . »
Nœud Intermediarité Louise 0 Daphné 0 Mathias 0 Elsa 1 Auriane 1