Transformées de Fourier usuelles

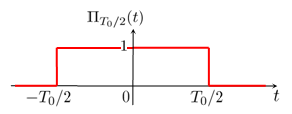
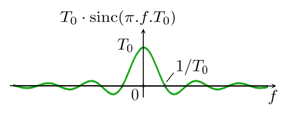
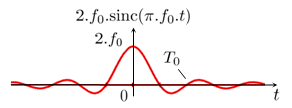
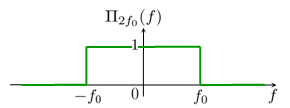
Le tableau qui suit présente les fonctions usuelles et leur transformée dans le cas où on utilise la convention la plus fréquente conforme à la définition mathématique.

Bibliothèque wikiversitaire

Intitulé : Transformées de Fourier usuelles

Formulaires

---

Toutes les discussions sur ce sujet doivent avoir lieu sur cette page.

Cet élément de bibliothèque est rattaché au département Outils mathématiques et informatiques pour la physique.

Transformée de Fourier	Transformée de Fourier inverse

Quelques unes des démonstrations sont données dans le chapitre : Série et transformée de Fourier en physique/Fonctions utiles.

Fonction	Représentation temporelle	Représentation fréquentielle
Pic de Dirac	$\delta (t)$	$1$
Pic de Dirac décalé de $t_{0}$	$\delta _{t_{0}}(t)=\delta (t-t_{0})$	$\mathrm {e} ^{-\mathrm {j} .2\pi .f.t_{0}}$
Peigne de Dirac $T_{e}={\frac {1}{f_{e}}}$	$\mathrm {III} _{T_{e}}(t)$	$\mathrm {III} _{f_{e}}(f)$
Fonction porte de largeur $T_{0}$	$\Pi _{{T_{0}}/2}(t)$	${T_{0}}\cdot \mathrm {sinc} (\pi .f.{T_{0}})$
Constante	$1$	$\delta (f)$
Exponentielle complexe	$\mathrm {e} ^{\mathrm {j} .2\pi .f_{0}.t}$	$\delta (f-f_{0})$
Sinus	$\sin(2\pi .f_{0}.t+\varphi _{0})$	${\frac {1}{2.\mathrm {j} }}\cdot \left(\mathrm {e} ^{\mathrm {j} .\varphi _{0}}\cdot \delta (f-f_{0})-\mathrm {e} ^{-\mathrm {j} .\varphi _{0}}\cdot \delta (f+f_{0})\right)$
Cosinus	$\cos(2\pi .f_{0}.t+\varphi _{0})$	${\frac {1}{2}}\cdot \left(\mathrm {e} ^{\mathrm {j} .\varphi _{0}}\cdot \delta (f-f_{0})+\mathrm {e} ^{-\mathrm {j} .\varphi _{0}}\cdot \delta (f+f_{0})\right)$
Sinus cardinal	$2\cdot f_{0}\cdot {\rm {sinc}}(2\pi .f_{0}.t)$	$\Pi _{2f_{0}}(f)$

^*Représentation du spectre d'amplitude