Intégration en mathématiques/Devoir/Encadrement du nombre e

1°  Pour tout entier naturel $n$, on considère l'application $f_{n}:\mathbb {R} \to \mathbb {R}$ définie par :

$f_{n}(x)={\frac {x^{n}\mathrm {e} ^{-x}}{n!}}$.

a)  Pour $n>0$, donner le tableau de variation de $f_{n}$, en distinguant les deux cas : $n$ pair et $n$ impair.

b)  Tracer, dans un repère orthonormal $\left(O,{\vec {i}},{\vec {j}}\right)$, les courbes représentatives des fonctions $f_{2}$ et $f_{3}$ ; on précisera la position relative de ces courbes.

c)  En revenant au cas général, montrer que, si $0\leqslant x\leqslant 1$, alors on a :

$0\leqslant f_{n}(x)\leqslant {\frac {1}{n!\,\mathrm {e} }}$.

2°  Soit :

$I_{n}(x)=\int _{0}^{x}f_{n}$.

a)  Calculer $I_{0}(x)$.

b)  À l'aide d'une intégration par parties, démontrer la relation de récurrence :

$I_{n}(x)-I_{n-1}(x)=-{\frac {x^{n}}{n!}}\mathrm {e} ^{-x}$.

c)  Démontrer que l'on a :

$I_{n}(x)=1-\mathrm {e} ^{-x}\left[1+{\frac {x}{1!}}+\cdots +{\frac {x^{n}}{n!}}\right]$,

c'est-à-dire : $I_{n}(x)=1-\mathrm {e} ^{-x}\left[\sum _{p=0}^{n}{\frac {x^{p}}{p!}}\right]$.

Quelle est la limite, pour $n$ fixé, de $I_{n}(x)$ quand $x$ tend vers $+\infty$ ?

3°  On pose $J_{n}=I_{n}(1)$.

a)  Démontrer que $0\leqslant J_{n}\leqslant {\frac {1}{n!\,\mathrm {e} }}$.

En déduire, en utilisant le calcul de $I_{n}$, que l'on a :

$0\leqslant 1-\mathrm {e} ^{-1}\left[\sum _{p=0}^{n}{\frac {1}{p!}}\right]\leqslant {\frac {1}{n!\,\mathrm {e} }}$

et

$\sum _{p=0}^{n}{\frac {1}{p!}}\leqslant \mathrm {e} \leqslant \left[\sum _{p=0}^{n}{\frac {1}{p!}}\right]+{\frac {1}{n!}}$.

b)  Quelle est la limite, quand $n$ tend vers $+\infty$, de $\sum _{p=0}^{n}{\frac {1}{p!}}$ ?

c)  En calculant $\sum _{p=0}^{5}{\frac {1}{p!}}$, donner le meilleur encadrement, permis par ce calcul, du nombre $\mathrm {e}$.

Corrigé

1. a) $f'_{n}(x)={\frac {\mathrm {e} ^{-x}x^{n-1}(n-x)}{n!}}$ (nulle en $0$ — comme $f_{n}$ — si $n>1$), $\lim _{+\infty }f=0$ et $\lim _{-\infty }f=+\infty$ si $n$ pair, $-\infty$ si $n$ impair.
   Si $n$ est pair, $f$ est décroissante jusqu'à $x=0$, puis croissante jusqu'à $n$, puis décroissante.
   Si $n$ est impair, $f$ est croissante jusqu'à $x=n$, puis décroissante.

   b)
   
   $f_{3}(x)>f_{2}(x)\Leftrightarrow x>3$.

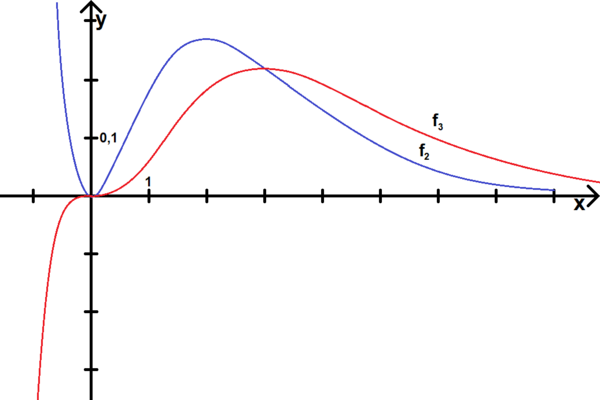
   c) Si $0\leqslant x\leqslant 1$ alors $0=f_{n}(0)\leqslant f_{n}(x)\leqslant f_{n}(1)={\frac {1}{n!\,\mathrm {e} }}$.

2. a) $I_{0}(x)=\left[-\mathrm {e} ^{-t}\right]_{0}^{x}=1-\mathrm {e} ^{-x}$.

   b) $I_{n}(x)=\left[-{\frac {t^{n}\mathrm {e} ^{-t}}{n!}}\right]_{0}^{x}+I_{n-1}$.

   c) Récurrence immédiate, et $\lim _{+\infty }I_{n}=1$.

3. a) L'encadrement de $J_{n}$ s'obtient en intégrant celui de $f_{n}$ sur $\left[0,1\right]$ obtenu dans la question 1.c.
   D'après la question 2.c, $J_{n}=1-\mathrm {e} ^{-1}\left[\sum _{p=0}^{n}{\frac {1}{p!}}\right]$.
   L'encadrement de $\mathrm {e}$ est alors immédiat.

   b) D'après le théorème des gendarmes, $\lim _{n\to \infty }J_{n}=\mathrm {e}$.

   c) $1+1+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}={\frac {326}{120}}$ donc ${\frac {326}{120}}\leqslant \mathrm {e} \leqslant {\frac {327}{120}}$.
   ${\frac {326}{120}}={\frac {163}{60}}\approx 2{,}717$ et ${\frac {327}{120}}={\frac {109}{40}}=2{,}725$, donc $\mathrm {e} \approx 2{,}72$.

Faites ces exercices : Fonction exponentielle/Annexe/Démonstration que la somme infinie de tous les inverses des k! est égale à e.