Recherche:Le temps dans la relativité restreinte ou la célérité du temps/Mathématique
Formalisme classique
La relativité restreinte est établie à partir de 2 postulats dans les référentiels galiléens. Le premier stipule que les lois de la physique y ont la même forme. Le deuxième définit que la vitesse de la lumière dans le vide est identique. Ils induisent les équations de Lorentz. Elles prédisent des phénomènes de dilatation des durées et de contraction des longueurs lors d'un déplacement:
Une représentation de l'espace-temps peut être analogue à celle de la figure 3. Le long des deux droites, tous les évènements sont 'simultanés'. A droite et à gauche, entre les droites, se trouvent l'espace-temps où les 'évènements' ne peuvent avoir lieu. En haut et en bas, entre les droites, se trouvent les 2 espace-temps des 'évènements' : Le futur et le passé. l'intersection des droites représente le présent. Cela résume et simplifie la représentation de Minkowski.
La droite x = ct relie l'espace au temps par une constante c. Mais c est aussi une célérité, ce qui suggère un déplacement. Au travers du postulat novateur (le temps se déplace), la seule altération apportée à la construction classique est la suivante : Le temps est orienté, il va du futur vers le passé. Ainsi, les droites sont orientées.
Formalisme novateur
Le formalisme classique est conservé, on y joint un concept novateur de déplacement du temps (phénomène physique filial du 'temps').
En cinématique, l'équation x(t)=Vt définit la position d'un objet se déplaçant à une vitesse V. Existe-t-il une entité susceptible de se déplacer constamment et immuablement à c. Comme supposer au chapitre précédent, une entité éligible est le temps.
Supposons que V(t) = c
Si je veux connaître la position du temps, j’obtiens simplement :
x(t) = ct (ou encore t = x(t)/c)
Considérons la classique expérience de pensée de la figure 1.https://commons.wikimedia.org/wiki/File:Laser_et_%C3%A9quations_du_temps.pdf
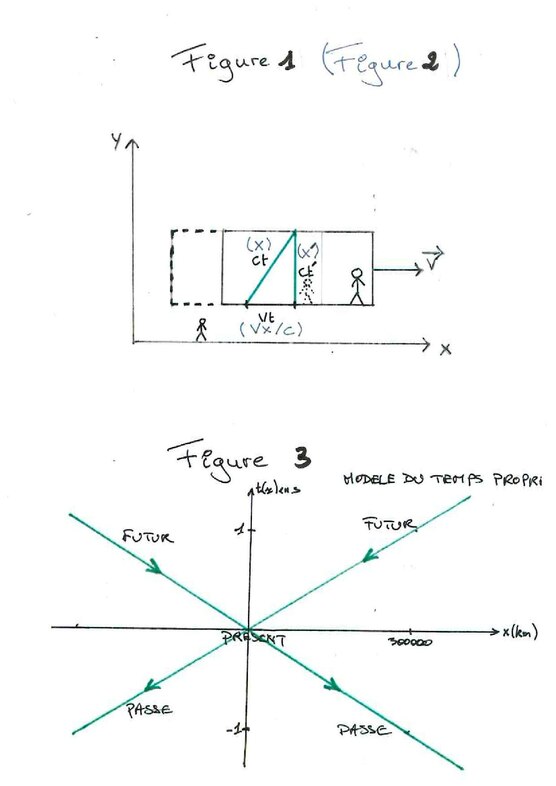
(Il s'agit de l'expérience d'un coup de laser orienté verticalement dans un vaisseau se déplaçant horizontalement). En appliquant Pythagore aux composantes de la figure, on obtient t = ɣt’. En imposant au temps de se déplacer à c (t = x(t)/c), on obtient la figure 2 et X de la figure correspond à x(t). En développant, on tombe sur l’expression x’(t) = x(t)/ɣ. La position du temps est contracté comme l'espace classiquement.
De même, t = -x(t)/c est aussi solution. Les 2 solutions sont représentées sur la figure 3. S’il existe un modèle géométrique, il doit satisfaire les 2 solutions. La deuxième solution vient du fait que quel que soit le signe de la solution, elle satisfait le théorème de Pythagore. (Les termes sont au carré). Elle permet au temps d'aller dans les 2 sens pour une même direction.
Spécificités du formalisme
Au travers du modèle du temps propre, la transformée supplémentaire x(t)² = c²t² simplifie le formalisme. Les paradoxes sont levés. De plus, elle n'engendre pas de courbure. La relativité devient géométrique. Cela a le mérite de se dessiner et d'être visuel.
Invariance relativiste
L'analogie entre notre transformée et l'expression de l'invariant relativiste x² + y² + z² - c²t² = x'² + y'² + z'² - c²t'² est immédiate. Cela signifie physiquement qu'une sphère de rayon ct pour un observateur extérieur est équivalente à une sphère de rayon ct' pour un observateur intérieur. La différence avec l'invariant relativiste est que ces sphères se dilatent dans le passé et se contractent dans le futur.
Autre formulation
Considérons l'invariant relativiste précédent, son expression permet de relier le temps à l'espace. Mais, dans notre espace-temps, le temps va du futur vers le passé en passant par le présent (t=0), c'est une variable qui va toujours dans le même sens. Simplement, l'espace suit le temps. Ainsi, l'espace se contracte dans le futur, est un point au présent et s'éloigne dans le passé. L'expression ainsi envisagée est moins glamour mais tout aussi exacte puisque espace et temps sont reliés. Cette notion de célérité de l'espace-temps simplifie et explique tout. C'est ce que propose de clarifier les expériences de pensée développées dans les chapitres à venir.

